•Time: September 25-28, 2019 (Arrival onSeptember 24, Tuesday)
•Location: Institute for Advanced Studyin Mathematics, Zijingang Campus, Zhejiang University (ZJU), Hangzhou, China
•Participating Institutions: EcolePolytechnique, Sorbonne Universite, Ecole Normale Superieure, MINES ParisTech and Zhejiang University
•Organize Committee (in alphabetical order):
Gang BAO(Zhejiang University)
Thierry CAZENAVE(Sorbonne University)
Gaëlle LEGOFF (Ecole Polytechnique)
Chuanhou GAO(Zhejiang University)
Min LI(Zhejiang University)
Weimin SHENG(Zhejiang University)
Xiang XU(Zhejiang University)
Ting ZHANG(Zhejiang University)
•Goal: French mathematics ranks amongthe top in the world. By 2018, French mathematicians account for 12 of thetotal 60 Fields Medal Winners. Almost all of the Fields Laureates have studiedor taught in Paris, making the top institutions there the cradle of the world’sbest mathematicians. ZJU is one of the top universities in China, withexcellent students and a distinguished tradition of mathematical research.ZJU’s "Chen-Su School" in the 1940s enjoys a high reputation in theinternational mathematical community. Currently, ZJU is striving to become aworld-class university with first-class mathematics. This forum aims to promoteall-round, strategic cooperation and exchange between ZJU and the topinstitutions in Paris in mathematical education and research.
•Invited Speakers (in alphabetical order):
AlessandroChiodo (Sorbonne University)
FrançoisGay-Balmaz (Ecole Normale Superieure)
VincentGiovangigli (Ecole Polytechnique)
JingRebecca Li (Ecole Polytechnique)
YvonMaday (Sorbonne University)
FrankPacard (Ecole Polytechnique)
Yongbin RUAN (ZhejiangUniversity, University of Michigan)
Speakers fromZhejiang University (to be confirmed)
•Agenda
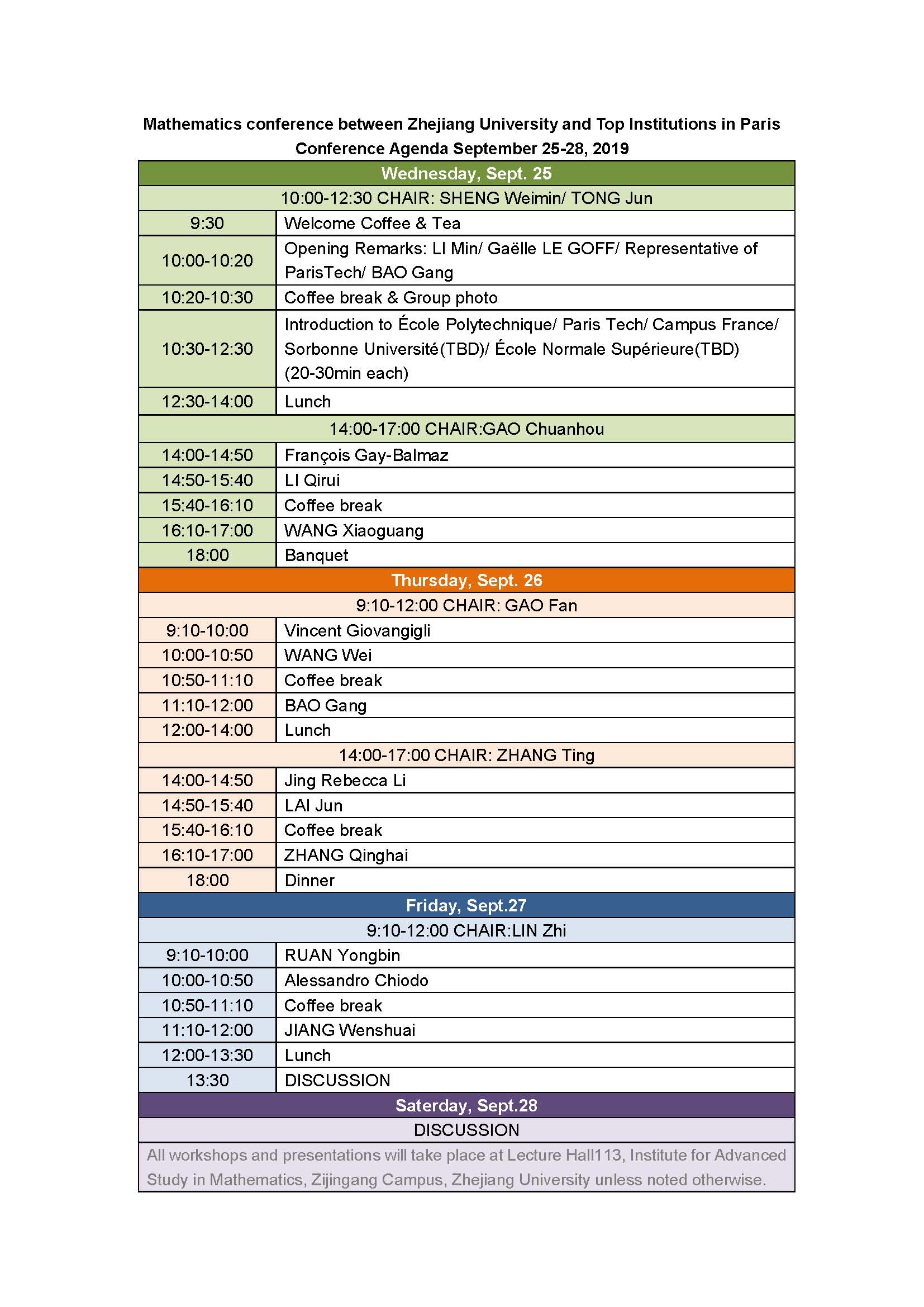
•Title &Abstract
Speaker: FrançoisGay-Balmaz (Ecole Normale Superieure)
francois.gay-balmaz@lmd.ens.fr
Title: Geometricdiscretization and geometric modeling in continuum mechanics
Abstract: Inthis talk we review some recent progresses made in the discretization andmodelling of fluid dynamics by using geometric variational methods.
Inthe first part, we use the geometric variational formulation of reversiblefluid dynamics on diffeomorphism groups to derive a structure preserving finiteelement discretisation for several fluid models used in geophysical fluiddynamics. Given a triangulation on the fluid domain, the discrete group ofdiffeomorphisms is defined as a certain subgroup of the group of linearisomorphisms of a finite element space of functions. As a consequence of theirstructure preserving nature, the resulting schemes exhibit an excellent longterm energy behavior and respect several conservation laws of the continuoussystem. We illustrate these properties with some examples from geophysicalfluid dynamics.
Inthe second part, we extend the variational formulation of reversible fluids tothe setting of nonequilibrium thermodynamics. The resulting variationalformulation extends the classical Hamilton principle to include irreversibleprocesses such as viscosity, diffusion, and heat transfer. We illustrate theefficiency of our variational formulation as a modeling tool by treating someexamples from geophysical fluid dynamics.
Speaker: Qirui Li (ZhejiangUniversity)
qi-rui.li@zju.edu.cn
Title:Regularity in Monge’s mass transport problem
Abstract: The optimal transportation problem was introduced by a French mathematician Gaspard Monge in 1781. Since then the problem has been extensively studied and more general costs are allowed. But for Monge's original cost, very little is known about the regularity. In this talk, we discuss the regularity in Monge's problem, and in particular show that, in two dimensional case, the optimal mapping is continuous. The talk is based on joint works with F. Santambrogio and X.-J. Wang.
Speaker: XiaoguangWang (Zhejiang University)
wxg688@163.com
Title: Newton's methods for polynomials: adynamical system viewpoint
Abstract: The talk consists of two parts. In thefirst part, I will give a brief introduction to the research works of ourdynamical system research group. In the second part, I will discuss theNewton's methods for finding roots of polynomials, from its history to recentprogress.
Speaker: VincentGiovangigli (Ecole Polytechnique)
vincent.giovangigli@polytechnique.edu
Title: Relaxation of internalenergy and volume viscosity
Abstract: We investigate the fast relaxationof translational and internal temperatures in nonequilibrium gas modelsderived from the kinetic theory. Strong solutions are investigated in thefast relaxation limit for ill prepared initial data. In the fast relaxationlimit the difference between the translational and equilibriumtemperatures becomes asymptotically proportional to the divergence of thevelocity field. This yields the volume viscosity term of the limitingone-temperature equilibrium fluid model. Numerical simulations are finallypresented of the impact of volume viscosity during a shock/hydrogen bubbleinteraction.
Speaker: Wei Wang(Zhejiang University)
wangw07@zju.edu.cn
Title: On the stability of current-vortex sheets in idealincompressible magneto-hydrodynamics
Abstract: In the first part of this talk, we will give a briefintroduction to the members and research works of the PDE group in ZJU. In thesecond part, we will discuss the stability of current-vortex sheets in idealincompressible magneto-hydrodynamics. It is well-known that vortex sheets forincompressible Euler equations are not stable (called Kelvin-Helmholtzinstability). However, in 1953, Syrovatskij derived a stability condition whichindicates that when the magnetic field is sufficiently strong, current-vortexsheets for magneto-hydrodynamics could probably be stable. We will present thelocal-in-time existence result of the solution for the incompressiblecurrent-vortex sheets under Syrovatskij's stability condition, which gives arigorous confirmation of the stabilizing effect of the magnetic field on theKelvin-Helmholtz instability.
Speaker: Gang Bao(Zhejiang University)
baog@zju.edu.cn
Title &Abstract: TBA
Speaker: Jing-RebeccaLi (Ecole Polytechnique)
jingrebecca.li@inria.fr
Title: Mathematical methods for diffusion magnetic resonance imaging(dMRI)
Abstract: Thecomplex-valued transverse water proton magnetization subject todiffusion-encoding magnetic field gradient pulses in a heterogeneous medium canbe modeled by the Bloch-Torrey partial differential equation with discontinuousinterface conditions. The diffusion MRI modeling problem is aboutquantifying tissue cell structure and membrane permeability from voxel levelsignals in multiple diffusion directions, diffusion times, and gradientmagnitudes. I will describe a Matlab-based simulation toolbox calledSpinDoctor that we developed to solve the forward problem and our recentprogress towards the inverse problem and parameters estimation.
Speaker: Jun Lai (ZhejiangUniversity)
laijun6@zju.edu.cn
Title & Abstract: TBA
Speaker: QinghaiZhang (Zhejiang University)
qinghai@zju.edu.cn
Title: MARS: AnAnalytic and Computational Framework for Incompressible Flows with MovingBoundaries
Abstract: Current methods such as VOF methods andlevel-set methods avoid geometry and topology by converting them intoproblems of numerical PDEs. In comparison, we try to tackle geometric andtopological problems with tools in geometry and topology. The firstpart of our MARS framework is the Yin space, a mathematical model forphysically meaningful material regions. Each element in the Yinspace is a Yin set, a regular open semianalytic set with boundedboundaries. Each Yin set is represented by a poset of orientedJordan curves so that its topological information (such as the Bettinumbers of a material region) can be extracted in constant time. Wefurther equip the Yin space with a simple Boolean algebra that isefficient and complete for arbitrarily complex topology.
In particular, non-manifold points on the fluid boundary, a keyproblem in studying topological changes, are handled naturally. The secondpart of MARS is the donating region theory in the context of hyperbolicconservation laws. For a fixed simple curve in a nonautonomous flow, thefluxing index of a passively advected Lagrangian particle is the total numberof times it goes across the curve within a given time interval. Suchindices naturally induce donating regions, equivalence classes of theparticles at the initial time. Under the MARS framework, many explicitmethods such as VOF methods and fronting tracking methods can be unifiedand proved to be second-order accurate. MARS also leads to new methods offourth- and higher-order accuracy for interface tracking and curvatureestimation.
The MARS framework can be further expanded with a fourth-order projectionmethod called GePUP for numerically solving the incompressibleNavier-Stokes equations (INSE). We have augmented GePUP to irregulardomains and are currently working on coupling GePUP with our newinterface tracking methods to form a fourth-order solver for INSE withmoving boundaries.
Speaker: Yongbin Ruan (Zhejiang university/University of Michigan)
ruan@umich.edu
Title: Verlinde/Grassmanniancorrespondence and quantum K-theory
Abstract: Morethan twenty years ago, Witten proposed an equivalence of two quantum fields governingVerlinde algebra (or the theory of stable bundles over a curve) and the quantumcohomology of Grassmannian. Motivated by Witten’s physical work and recentrevival of quantum K-theory, we proposed a K-theoretic version of so-calledVerlinde/Grassmannian correspondence. Furthermore, the recent interpretation ofquantum K-theory as a 3d quantum field theory opens a door
to much larger area of physics and mathematics. Wewill first review the new ingredient of level structure in quantum K-theory andsurprising appearance of mock theta function. Then, we will present an approachto the proof of correspondence using wall-crossing technique. This is a jointwork with Ming Zhang.
Speaker: AlessandroChiodo (Sorbonne University)
alessandro.chiodo@imj-prg.fr
Title: Spin graphs and quadraticforms
Abstract: Graphs areelementary objects in combinatorics for which a deep theory of divisors, ranksand Riemann-Roch formulae has been developed in full analogy with the theory ofRiemann surfaces. In many ways spin graphs lack an analogous treatment. ForRiemann surfaces the rank of spin structures exhibit a beautiful dichotomybetween even and odd structures governed by a quadratic form. For graphs, thepicture so far only exhibited one distinguished spin structure, but thequadratic form does not generalize. We study thick graphs (graph with thickenededges) which shed new light on the theory of ranks of graph. They allow us toprovide new formulae for the ranks in the classical case. Finally they allow usto single out a class of (hyperelliptic) graphs where the theory works exactlyas it does for Riemann surfaces. This is work in progress with MarcoPacini.
Speaker: Wenshuai Jiang (ZhejiangUniversity)
wsjiang@zju.edu.cn
Title: On the manifolds with Ricci curvaturebounds
Abstract: In the first part of the talk, wewill introduce our differential geometry group(W. Sheng, Q. Xia,J. Wu, F. Wang, Q. Li ) and briefly discuss some works of them. In the second part, we will discuss the study of manifolds with Ricci curvaturebounds which is based on jointed work with Jeff Cheeger and Aaron Naber.



